18
avril 1978
(p1->)Venez
un peu, parce que vous m’avez envoyé des choses. Je voudrais que, les choses
que vous m’avez envoyées, vous les commentiez comme ça, une par une, parce
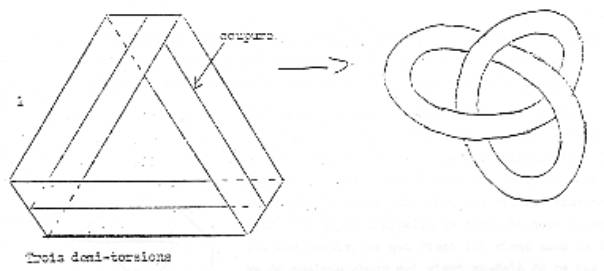
que ça ne va pas. Je vous signale que ce que je vous ai dessiné la dernière
fois, sous la forme de cette bande que j’ai faite du mieux que j’ai pu, si
on la coupe en deux, le résultat – si on la coupe en deux comme ceci- le résultat
est ce qu’on appelle un nœud à trois, c’est-à-dire quelque chose qui
se présente comme ça. C’est bien entendu, tout à fait frappant. Ici, c’est ce qu’on appelle une bande de Moebius. Je la redessine pace que ça vaut la peine de s’apercevoir que grâce à ce qu’on appelle l’élasticité….la bande de Moebius se dessine comme ça. En d’autres termes, on retourne ce qui apparaît sous cette forme.
La forme présente est celle qui apparaît sur la couverture de Scilicet.
Mais la véritable bande de Moebius est celle-ci. Et il y a ce que très légitimement
Jean Claude Terrasson qui est là et qui m’aide, ce que très légitimement
Jean Claude Terrasson appelle une demi-torsion et là, sous la forme où j’ai
fait fonctionner la
(p2->)
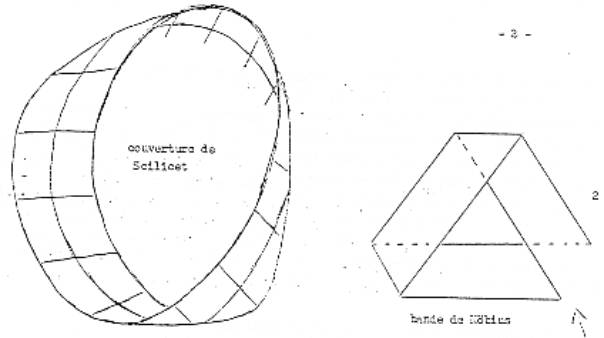
dernière
fois –puisque c’est ce que je vous ai dessiné la dernière fois- il y a
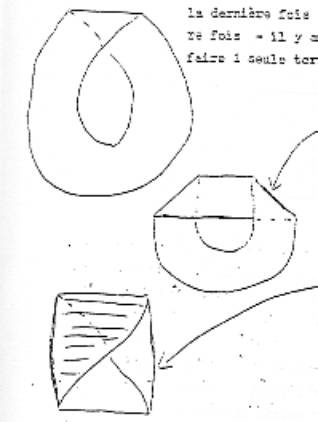
trois demi-torsions. Par contre, il est possible de faire 1 seule torsion.
C’est ce qui est manifesté dans la figure 2 où il y a effectivement 1 seule
torsion. La figure 2 peut également se figurer ainsi. Ca c’est une figure à
une seule torsion, elle est équivalente à la figure suivante, c’est à dire
que ceci, si nous figurons l’intérieur ici, ceci est réalisé communément
par ce qu’on appelle le tore. Si nous faisons ici une boucle, ce qui vient ici
vient sous la forme de quelque chose qui vient au-delà de ce que j’appelle
l’axe du tore, c’est ça qui vient dans l’axe du tore et c’est ça qui
fait le tour du tore. Je vous prie à cette occasion de le vérifier, et vous
verrez que la torsion, la torsion complète dont il s’agit est exactement équivalente
à ce que Jean Claude Terrasson appelle une torsion complète. C’est ça qui
est réalisé dans le tore dont nous n’avons évidemment….La torsion complète
est tout ce qu’on peut faire sur un tore, ce qui n’est bien entendu pas
surprenant, parce qu’il n’y a aucun moyen d’opérer, autrement sur un
(p3->)
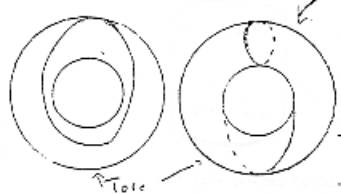
tore.
Si sur un tore vous dessinez quelque chose qui coupe bien sûr, qui coupe en
passant ce qu’on appelle derrière le tore, qui revient en avant et qui
repasse derrière le tore, ce que vous obtenez, c’est quelque chose qui est
comme ça et qui s’achève de la façon suivante, c’est à dire que cela
redouble le nœud qui s’entoure autour du tore. En d’autres termes ce qui
vient ici, est très précisément ce qui se passe autour de ce que j’appelle
l’axe. Donc ceci équivaut à deux torsions. Ici une torsion et là deux
torsions.
Je vais prier maintenant Jean Claude Terrasson, de bien vouloir prendre
la parole pour me commenter ses figures, ses figures qu’il a faites là.
Ceci est une bande de Moebius :
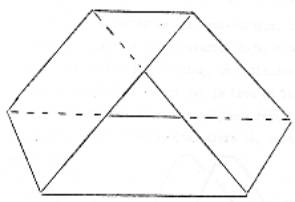
J.C TERRASSON :
Alors on peut poser le problème de savoir comment on pourrait paver
l’espace, ou paver le plan régulièrement avec des bandes de Moebius
aplaties, c’est à dire mises à plat. Alors le problème, c’est comment
est-ce que je pourrais paver régulièrement le plan en aplatissant des bandes
de Moebius,… enfin des bandes, c’est à dire on peut commencer par la bande
à zéro torsion qui est…
(p4->)
Si on dessine uniquement les bords, on les dessine comme ça, ils ne
sont liés que par le fait que la bande a une certaine matérialité pour lier ces deux bords. Bon alors, pour mettre cette figure à plat, pour l’aplatir et obtenir quelque chose qui pave régulièrement le plan, c’est à dire un polygone régulier – enfin, il n’y en a pas des masses, il y a que l’hexagone, le carré et le triangle équilatéral- pour ça j’ai une solution très simple qui est de coller les deux bords ensemble, enfin coller un bord, accoler un bord à lui-même et aplatir c’est à dire que si c’est hachuré là où la surface vient deux fois l’une sur l’autre, bon c’est ça. Donc j’obtiens un carré, bon là ce n’est pas un carré, mais ça pourrait être, à condition que ma bande ait le double de la longueur et de la largeur et j’obtiens un carré.
A partie de une demi-torsion, là le problème va être plus compliqué ; mais ce qu’on remarque déjà, c’est que chaque fois, on obtiendra un polygone régulier, sans trou, c’est à dire ce qui est le trou de la bande trouve un moyen de se résorber pour obtenir un polygone régulier et ça sera même le seul que je pourrai obtenir. Bon, alors là, cette figure là si j’en dessine
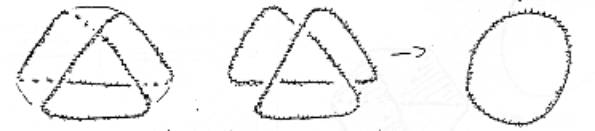
le bord, c’est ça, c’est à dire on voit que ça tient noué… comme la première figure, le bord ne tient dans sa position de torsion que par rapport au fait que la bande est matérialité aussi.
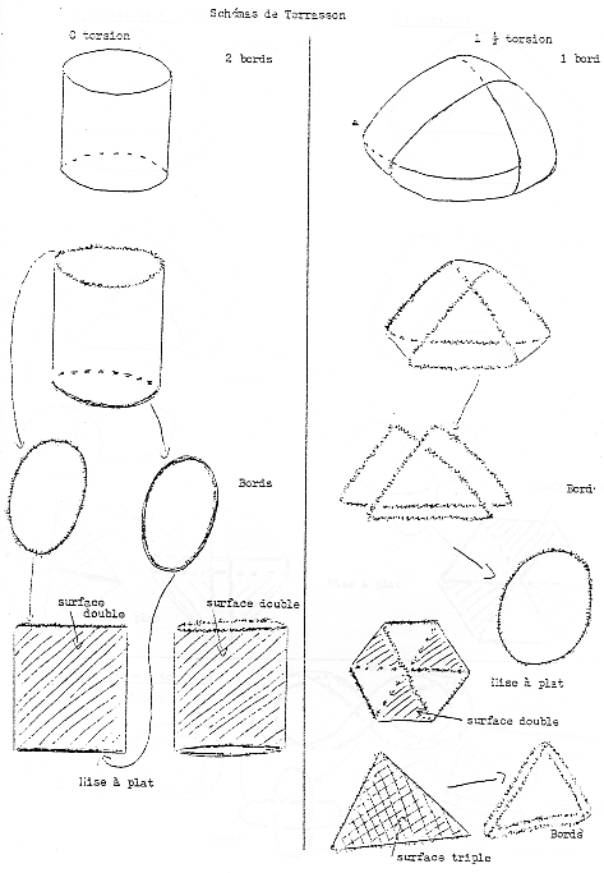
(p5->)Ce
sera plus vrai à partir de ces bandes là où les bords se tiennent par eux même
en dehors de toute matérialité de la bande. Alors ça c’est, c’est la mise
à plat du tore à une
demi-torsion. Alors je dessine le bord de la bande et en pointillé évidemment,
là où il passe dessous et hachuré l’endroit où la surface se recouvre. Bon
alors cette bande
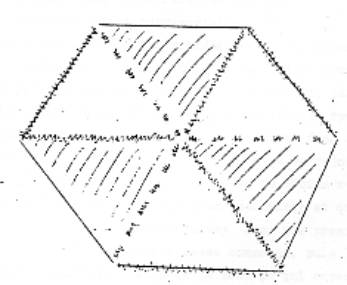
comme toutes celles qui seront de hexagones, pour obtenir un hexagone régulier, il faut que les proportions ça soit : largeur je prends 1 de largeur, la longueur ça sera racine de 3 : l=1 ; L= √3 ; bon on ne va pas entrer la dedans. Alors ce qui se passe à la bande à demi-torsions, c’est à dire à 1 torsion, c’est-à-dire 1 bande à deux bords, voilà la
manière dont les bords du trou, les bords de la bande se nouent entre eux, c’est à dire que là ils n’ont plus besoin de la matérialité de la bande pour maintenir leur nouage, c’est bien pour ça qu’on passe au tore, comme disait Lacan tout à l’heure.
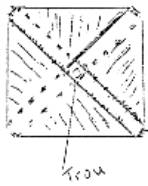
Alors
cette figure-là se remet à plat dans le carré. Mais pour rendre ces figures là
plus lisibles….là aussi le bord vient s’accoler à lui-même, c’est à
dire là il est deux fois, alors il faudrait que je le dessine avec un petit écartement
pour rendre la chose visible. En dessinant, en hachurant toujours là où ça se
recouvre, voilà avec un petit écartement pour voir comment le trou, les bords
du trou se nouent entre eux. Il y a cette figure qui est donc recouverte, où la
surface se recouvre dans la totalité, cette figure est un carré et à partir
de ce moment là, ce n’est plus un carré là, mais c’est un carré qui est
obtenu avec une bande dont la longueur est 4 fois la largeur L=4l
(Elleégalequatreelles)
(p6->)
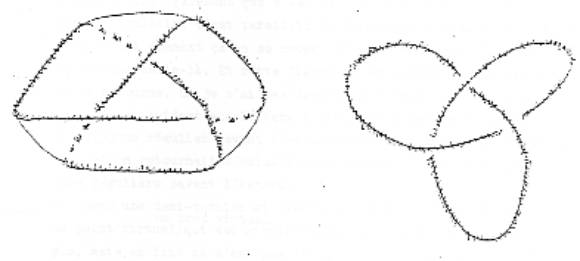
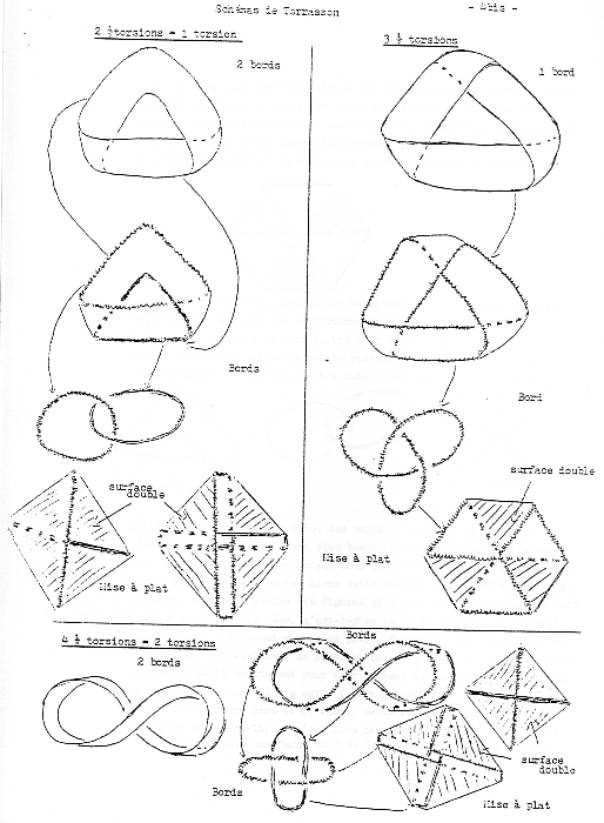
Alors on passe à trois demi-torsions, c’est-à-dire que là le dessin du bord de la bande c’est ça. Je peux encore mettre à plat cette figure là, cette bande-là, bon c’est pareil, je dessine le bord
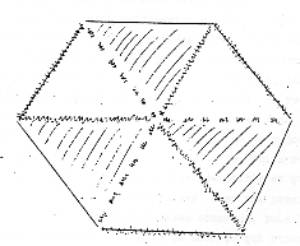
visible
du trou, et j’obtiens cette figure là, c’est-à-dire que je le fais avec
une bande qui a les mêmes, les mêmes proportions que celles-là, toujours.
La bande à quatre, c’est la bande à quatre demi-torsions, c’est à
dire à deux torsions, bon, elle noue ses bords de cette manière là, (p7->)
c’est
à dire comme ça, c’est le deuxième nœud… Et on pourrait dire
également que c’est le tore à deux trous et celle-là, je peux encore
l’aplatir. C’est pareil, il faudrait que je dessine le bord du trou. Voilà
comment ça va se nouer, et vous voyez que c’est la même figure que celle là.
Et cette figure là est identique à elle-même si on la retourne. Là je n’ai
pas dessiné le tore à cinq demi-torsions mais il est évident que le tore à
cinq demi-torsions ne va pas faire un polygone régulier pavant
l’espace ; ça il n’y aura plus moyen. Mais si on retournait à celui
à 6, on pourrait encore refaire une figure régulière pavant l’espace.
J.VAGARRIGUE-
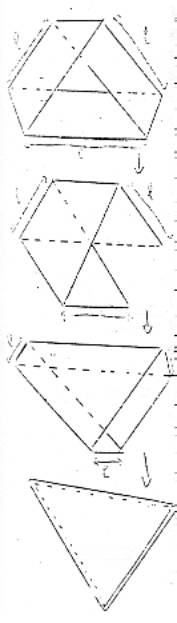Avec une demi-torsion et avec trois demi-torsions, tu as
toujours un point virtuel, un trou virtuel qui est un point là qui est tout
comme un petit triangle, mais en fait ce n’est pas obligatoire pour une seule
torsion et tu peux la réduire à la dimension d’un triangle….
Tu
as cette représentation là actuellement et tu as le bord qui décrit un schéma
là, comme ça, avec le bord qui est ici, qui passe derrière et tu as le bord là
qui repart devant, et qui fait ce schéma. Mais enfin on peut réduire ces trois
bords à n’être plus rien. Alors si tu réduis ces bords à n’être plus
rien, tu obtiens une forme qui est triangulaire que je ne fais pas tout à fait
triangulaire pour que ce soit plus facilement représentable et/où tu as ce
bord en fait qui va… ; ce
n’est pas facile à représenter, et où tu as en fait ce bord là, il viendra
ici comme ça, puis ça va passer derrière, là comme ça et puis ça va
revenir sur le devant, ce bord-ci, là, il va là, ce petit côté-là qui se réduit
à rien, il est ici, ça repasse derrière et ça rejoint ce bord-là, celui-là
va se trouver donc en haut et puis ç va revenir ici pour repasser derrière et
ça va rejoindre…ici...le troisième. Et
alors là il y a une bande de Moebius réduite à sa plus simple expression et
qui n’est plus réductible et qui a la forme d’un triangle à trois sections
successives avec une première qui est représentée par cette bande qui passe
comme ça, puis la seconde – là ça va passer derrière- et puis la seconde
qui repasse et qui se replie une troisième fois pour repasser derrière. Et en
fait ce dallage que tu fais ici avec un hexagone, tu peux le faire avec un
triangle, mais c’est une autre forme beaucoup plus simple en fait de dallage.
Et tu as la disparition que tu supposais presque obligatoire de ce trou virtuel
qui disparaît avec cette représentation-là. Voilà, c’est ce que je voulais
dire. C’est une autre interprétation.
(p8->)
TERRASSON : Pourquoi
j’ai fait ces représentations-là et pas celles-là ? C’est parce
qu’ici, j’ai au maximum une double épaisseur et une simple épaisseur et
que ça, je peux évidemment le représenter, comme ici d’ailleurs, par les
pavés dont je veux paver le plan. Et alors ça me…..
J.LAGARRIGUE :
Ici° tu n’as pas le trou virtuel qui traverse le
plan, vu que le seul trou est
°=
0 torsions
est un trou qui est vertical comme ça, comme une manche et ici, à cette
| représentation comme ici tu as toujours un trou qui est virtuel, qui est ici un point par lequel tu peux passer une aiguille, une épingle, et qui disparaît dans cette représentation (Schéma p.7) où tu as les trois qui se recouvrent absolument et qui est la forme en fait la plus réduite possible d'une bande de Moébius avec une seule demi-torsion et qui est une représentation qui est beaucoup plus réduite que celle-ci parce que tu élimines en fait cet effet d'hexagone, qui est un effet artificiel si on peut dire, qui n'a pas de raison d'être particulière. Sa seule raison d'être de forme de la bande de Moebius a une seule demi torsion, c'est en fait la forme triangulaire et c'est celle-là. Et cette forme là, tu ne peux pas l'obtenir avec la seconde bande de Moebius qui est la bande de Moebius à trois torsions où là l'existence de ce trou virtuel central est absolument obligatoire. Ca se fabrique très bien, ça d'ailleurs, avec une bande de papier.... | |
LACAN : |
Lacan
: L'intérêt de cette réflexion est que, également pour la
bande de Moebius, ce que j'ai dessiné la dernière fois, l'amincissement
de ce dont il s'agit, permet de maintenir la forme qui aboutit au noeud à
trois et ceci, je veux dire la bande de Moebius, comme il est bien connu,
la bande de Moebius divisée en deux fait un huit ; si mon souvenir est
bon, ce huit recoupé en deux fait une forme comme ceci, c'est-à-dire
quelque chose d'enlacé, si mon souvenir est bon. Je crois que mon
souvenir est bon.
J.L : Je crois que ça donne une formation qui a des caractéristiques comme ça. Lorsqu'on divise deux fois une bande de Moébius, on obtient une bande qui ressemble à ça, qui est de ce type-là, avec une bande comme ça qui est nouée par une sorte de tissage et qui n'est pas simple
Lacan : Je crois en effet que ce sont deux anneaux séparés qu'on obtient avec la bande de Moebius. Il y a quelque chose qui me paraît pourtant pas claire c'est votre double torsion, comment obtenez-vous cette figure-là ?
|
| TERRASSON | : En
aplatissant une bande de Moebius, une bande à une torsion, en
l'aplatissant, c'est-à-dire en faisant une demi-torsion à chaque fois,
elle prend cette forme-là. (discussion inaudible) |
| LACAN | :
En quoi ici les deux bord font-ils enlacement ? Car en fait c'est un fait
qu'ils font enlacement.
Ils font enlacement. |
| TERRASSON | : C'est la première bande dont les bords s'obtiennent par eux-même en dehors du fait du sort de la bande... |
| LACAN | : Les deux bords font enlacement. |
| TERRASSON | : C'est le premier enlacement de bords. On peut continuer. Il y a toute la série des enlacements. |
| LACAN | : Hein ? |
| TERRASSON | : Il y a toute la série des enlacements de bords.... |
| LACAN | : Je
vous fais mes excuses. Il y a un moyen de faire un noeud borroméen avec
le noeud à 3. Pourtant la question est de savoir s'il y a un autre moyen
de faire un noeud borroméen avec le noeud à 3. Si on groupe les 3, il
est bien évident que ce qu'on obtiendra ce sera la même chose, que ce
qu'on obtient avec la bande de Moébius. Est-ce qu'il y a moyen, en
décalant ce noeud à trois - c'est à ça que je ma suis escrimé ce
matin - en décalant ce noeud à 3, est-ce qu'il y a une moyen en
déplaçant ce noeud à 3 de faire qu'on puisse passer sous le second
noeud à 3 qui est légèrement décalé, qu'on puisse passer sous,
puisque c'est ça la définition du noeud borroméen, qu'on puisse passer
sous celui qui est dessous, et sur celui qui est dessus. C'est ce
que je vous propose de mettre à l'épreuve, puisque je n'ai pas pu le
mettre à l'épreuve moi-même ce matin. Il faut, d'autre part, bien se
dire que ce noeud à 3 lui-même se divise en 2, je veux dire qu'il est
susceptible d'être coupé, coupé par le milieu, et que ça donne un
certain effet que je vous propose également de mettre à l'épreuve.
Ceci nous promet pour la séance du 9 mai quelques résultats auxquels je m'efforcerai moi-même de donner une solution
|
note: bien que relu, si vous découvrez des erreurs manifestes dans ce séminaire, ou si vous souhaitez une précision sur le texte, je vous remercie par avance de m'adresser un email. Haut de Page