|
Lorsqu'un pilote d'avion veut aller d'un endroit à l'autre de la terre, il doit établir un itinéraire. S'il n'a pas besoin de faire d'escale, il va choisir le chemin le plus court car il consommera moins de carburant. S'il prend une carte aérienne ordinaire5, et qu'il trace une droite, et bien il ne choisira pas la route la plus courte.
En général une droite sur une carte ne suit pas le chemin le plus court sur le terrain. Le chemin le plus court pour aller d'un point à un autre de la terre -- ou de toute surface courbe -- est ce qui s'appelle une géodésique ou un grand cercle.
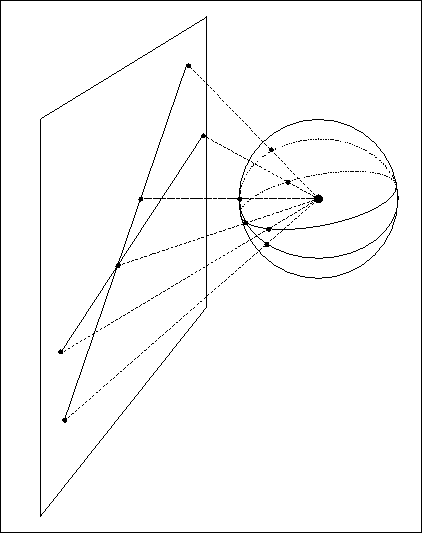
Il serait plus simple pour ce pilote de disposer d'une projection dans laquelle une géodésique se présente sous la forme d'une droite sur la carte. Cette projection existe, elle s'appelle la projection azimutale gnomonique. Derrière ce nom se cache tout simplement la figure qu'on obtient en projetant une sphère sur un plan en prenant comme centre de projection le centre de la sphère. Dans cette projection chaque grand cercle apparaît comme une droite du plan. Chaque droite est une droite projective.
Pour rendre sensible cette réalité, imaginez-vous installé au centre d'une sphère transparente, sur laquelle sont dessinés de nombreux grands cercles (des méridiens entre autres). Tous ces cercles sont centrés sur le centre de la sphère; si je suis sur ce centre je les verrai comme des droites. Ils se projetteront comme tels sur un plan.
Je n'en dirai pas plus sur ce point, observez la figure ici. Pour ce qui nous intéresse, il suffit de se rappeler que ces cartes sont des portions de plan projectif.