|
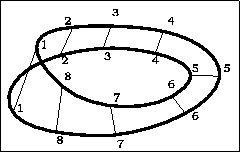
Il est possible de rendre compte du plan projectif également d'une autre façon. Pour cela il faut partir d'un anneau de Möbius dont le bord serait en fil de fer et la surface faite d'un grand nombre d'élastiques tendus comme cela est présenté figure ici. Par les déformations continues des figures ici, ici et ici on atteint la forme de la figure ici.
En imaginant une infinité d'élastiques formant ainsi un plan, un F se retrouve tête-bêche et en miroir quand il évolue le long d'un diamètre. Je peux suturer un disque sur le cercle de la figure ici. Ce disque est figuré par la portion de plan qui sépare le cercle et le cadre du dessin. Quand le F parcourt le disque il ne peut plus se superposer à la forme précédente.
La surface suturée est un plan projectif, la surface à un bord est un anneau de Möbius qui peut ensuite être présentée en cross-cap comme dans la figure ici4.
Cette construction est décrite dans l'ouvrage de Stephen Barr Experiments in Topology. [Bar89, pp 80-82]